Let ![]() .
.
- Prove that
 is strictly increasing on
is strictly increasing on  .
. - If
 , solve the equation
, solve the equation
![Rendered by QuickLaTeX.com \[\cos^2 x \cdot f \left ( \tan x \right ) + \sin^2 x \cdot f \left ( \cot^{22} x \right ) =0\]](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-d9a4b706cd26864552ef288b57da561b_l3.png)
Solution
- It is
 . However, recalling that
. However, recalling that
![Rendered by QuickLaTeX.com \[\ln x \geq 1 - \frac{1}{x} \quad \text{foreach} \quad x>0\]](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-d209fbca41bca8fa8cc154ecce0825d2_l3.png)
we conclude that
 is strictly increasing.
is strictly increasing. - We note that

On the other hand,
 and hence:
and hence:
A site of university mathematics
Let ![]() .
.
![]()
Solution
![]()
we conclude that ![]() is strictly increasing.
is strictly increasing.

On the other hand, ![]() and hence:
and hence:

Evaluate the product
![Rendered by QuickLaTeX.com \[\Pi = \prod_{k=1}^{n}\frac{(2k)^4+(2k)^2+1}{(2k-1)^4+(2k-1)^2+1}\]](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-d47de6f97187884876e1fbbb27b2625c_l3.png)
Solution
We are making use of the identity
![]()
Hence,
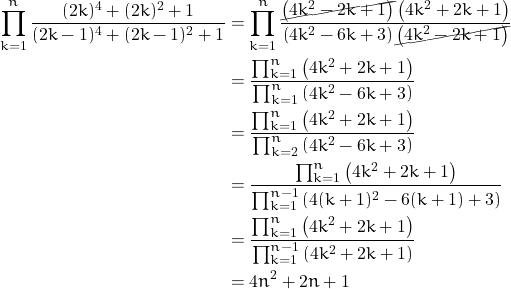
Let ![]() be a strictly increasing sequence of positive integers. Prove that the series
be a strictly increasing sequence of positive integers. Prove that the series ![Rendered by QuickLaTeX.com \displaystyle \mathcal{S} = \sum_{i=0}^{\infty} \frac{1}{\left [ a_i, a_{i+1} \right ]}](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-bacf586c1c8e3dc339002bfb7fcc3db5_l3.png) , where
, where ![]() denotes the least common multiple, converges.
denotes the least common multiple, converges.
Solution
We have successively:
![Rendered by QuickLaTeX.com \begin{align*} \sum_{i=0}^{\infty} \frac{1}{\left [ a_i, a_{i+1} \right ]} &= \sum_{i=0}^{\infty} \frac{\left ( a_i,a_{i+1} \right )}{a_i a_{i+1}} \\ &\leq \sum_{i=0}^{\infty} \frac{a_{i+1} - a_i}{a_i a_{i+1}} \\ &= \sum_{i=0}^{\infty} \left ( \frac{1}{a_i} - \frac{1}{a_{i+1}} \right ) \\ &= \frac{1}{a_0} - \lim_{N \rightarrow +\infty} \frac{1}{a_N} \end{align*}](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-ec01d6853c868f2e46d40e0bcb1c2ea3_l3.png)
Let ![]() . We define the sequence
. We define the sequence ![]() . Prove that
. Prove that
![]()
Prove that
![Rendered by QuickLaTeX.com \[\prod_{n=1}^{\infty} \left (1 + 2e^{-n \pi \sqrt{3}} \cosh \frac{n \pi}{\sqrt{3}} \right ) = \frac{\exp \left ( \frac{\pi \sqrt{3}}{18} \right )}{\sqrt[4]{3}}\]](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-cdc9835bb5af97ed9fffbb794129579b_l3.png)
Solution
Let ![]() and
and ![]() . Hence,
. Hence,
![Rendered by QuickLaTeX.com \begin{align*} \prod_{n=1}^{\infty} \left (1 + 2e^{-n \pi \sqrt{3}} \cosh \frac{n \pi}{\sqrt{3}} \right ) &= \prod_{n=1}^{\infty} \left ( 1 + q + q^{2n} \right ) \\ &= \frac{\prod_{n=1}^{\infty} \left ( 1 - q^{3n} \right )}{\prod_{n=1}^{\infty} \left ( 1 - q^n \right )} \\ &= \exp\left ( - \frac{i \pi \tau}{6}\right ) \frac{\eta(3\tau)}{\eta(\tau)} \\ &= \exp\left ( - \frac{i \pi \tau}{6}\right ) \frac{\eta \left ( - 1/\tau \right )}{\eta(\tau)}\\ &= \exp\left ( - \frac{i \pi \tau}{6}\right ) \sqrt{-i \tau} \\ &= frac{\exp \left ( \frac{\pi \sqrt{3}}{18} \right )}{\sqrt[4]{3}} \end{align*}](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-e72f41b960e6bdb7c06771a07cd9d377_l3.png)