Evaluate the sum
![Rendered by QuickLaTeX.com \[\sum_{k=0}^n \binom{n}{k}\frac{k!}{(n+1+k)!}\]](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-7949829aadf864616c759d1d6f37f398_l3.png)
Solution
We have successively
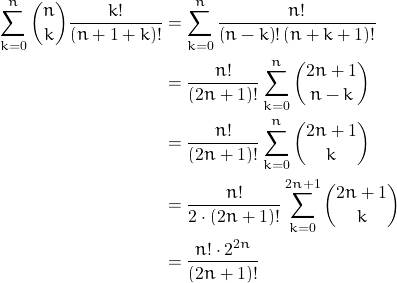
A site of university mathematics
Evaluate the sum
![Rendered by QuickLaTeX.com \[\sum_{k=0}^n \binom{n}{k}\frac{k!}{(n+1+k)!}\]](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-7949829aadf864616c759d1d6f37f398_l3.png)
Solution
We have successively
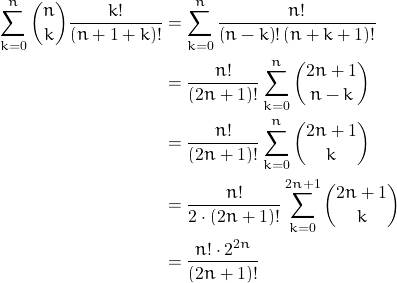
Prove that
![Rendered by QuickLaTeX.com \[\sum_{n_1=1}^{n-1} \sum_{n_2=1}^{n_1-1} \sum_{n_3=1}^{n_2-1} \cdots \sum_{n_m=1}^{n_{m-1}-1} 1 = \binom{n-1}{m}\]](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-25ee265bf7a9d75c2251289302057bb3_l3.png)
Solution
The binomial coefficient in the RHS enumerates the subsets ![]() of size
of size ![]() of
of ![]() . The LHS does the same thing, but choosing first the largest element
. The LHS does the same thing, but choosing first the largest element ![]() of
of ![]() , then its second-to-largest element
, then its second-to-largest element ![]() , until choosing its smallest element
, until choosing its smallest element ![]() .
.
Let ![]() denote the Möbius function and
denote the Möbius function and ![]() denote the floor function. Prove that:
denote the floor function. Prove that:
![Rendered by QuickLaTeX.com \[n! = \prod_{j=1}^{\infty} \prod_{i=1}^{\infty} \left ( \left \lfloor \frac{n}{ij} \right \rfloor! \right )^{\mu(i)}\]](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-051d390cacf02f7f0985573723edddbe_l3.png)
Solution
The RHS equals

since ![]() for
for ![]() .
.
For a rational number ![]() that equals
that equals ![]() in lowest terms , let
in lowest terms , let ![]() . Prove that:
. Prove that:
![]()
Solution
First of all we note that
![Rendered by QuickLaTeX.com \[F(s) = \sum_{x \in \mathbb{Q}^+} \frac{1}{f^s(x)} = \sum_{\substack{a,b=1 \\ \gcd(a, b)=1}}^{\infty} \frac{1}{\left ( ab \right )^s}\]](https://www.math.tolaso.com.gr/wp-content/ql-cache/quicklatex.com-06ec1c91de76d878cb19ee21f945d56c_l3.png)
Moreover for ![]() we have that
we have that

Hence for ![]() we have that
we have that
![]()